CUET Results 2022: UGC chairman explains how NTA prepared CUET scorecard

This raises the question of how to compare the scores of students who write tests for the same subject on different days. It needs to be ensured that the admissions are given based on a score that accurately compares the performance of the students. Therefore, CUET UG percentiles cannot be used for admissions.

Unlike CUET UG, other entrance examinations are limited to fewer subjects. In single-session entrance tests, one common statistically established method is to transform the raw marks into a common uniform scale using the percentile method so that the performance of students can be compared to each other.

But in entrance tests such as CUET UG, since the test is conducted on different days and in multiple sessions for the same subject, it will give rise to multiple percentiles for each group of students. Comparing their performance using only percentiles will, therefore, become difficult.

In addition to the above difficulty, in subjects such as sports or fine arts, some weightage (e.g. 25%) is given to the skill component by some universities. But, adding raw marks of the skill component and the remaining weightage (75%) of percentile cannot be done to prepare the rank list because it would be like adding oranges to apples.

A solution to this situation is the use of a method called the ‘equipercentile method’. In this method, normalised marks of each candidate are calculated using the percentiles of each group of students in a given session across multiple days for the same subject.

In the equipercentile method, we use the same scale for all candidates independent of which session they have appeared in a given subject making their performance comparable across sessions. These normalised marks of the candidates in different sessions in a given subject can be used in the same way we use the raw marks of a conventional single-session examination. Therefore, in a particular university, if the raw marks of the skill component has a certain weightage (e.g. 25%), it can be added to the remaining weightage (e.g. 75%) of the normalised marks to prepare the rank list. What is important to note here is that for each subject for which examination is held in multiple shifts, raw marks are converted into normalised marks on a common scale.

To calculate the normalised marks across different sessions in a given subject, first we need to find the percentile of each group of these students for each shift using the raw marks they have scored.

Let us say in a given shift, 100 students have appeared for the test. We sort their marks in decreasing order. Let us assume that one student among these 100 students has scored 87% marks. Now let us assume that 80 out of 100 students have secured less than or equal to 87% marks. The percentile of this student with 87% marks would be 80/100=0×8. The percentile so calculated will always be between 0 and 1 and it is usually rounded off to the requisite number of decimal places.

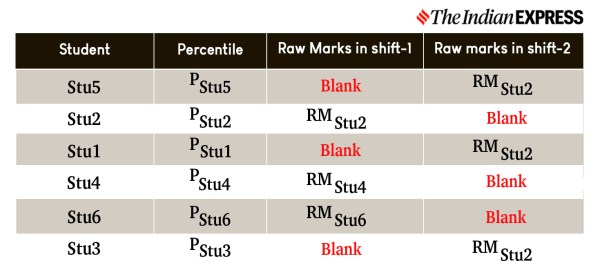
Let us now assume that there are six students (Stu1, Stu2, Stu3, Stu4, Stu5, Stu6). Three of them (Stu2, Stu4, Stu6) have taken the test in shift-1 and the remaining (Stu1, Stu3, Stu5) in shift-2 but all in the same subject.  Using the raw marks of these students, first the percentiles (PStu1 , PStu2 , PStu3 , PStu4 , PStu5 , PStu6) of these six students in a given subject are calculated and are sorted in decreasing order. Their Raw Marks (RMStu1 , RMStu2 , RMStu3 , RMStu4 , RMStu5 , RMStu6 ) in the test in each shift are also noted corresponding to their percentiles.

Let us assume that the percentiles in descending order are as follows:

PStu5 > PStu2 > PStu1 > PStu4 > PStu6 > PStu3

(Graphics by Abhishek Mitra)

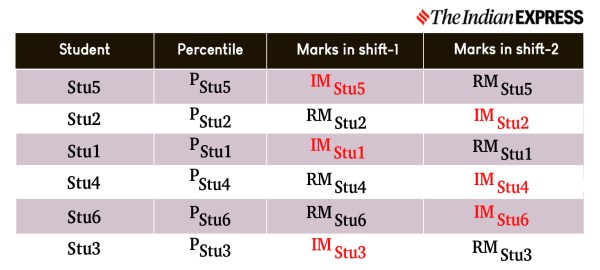
Since some students (Stu2, Stu4, Stu6) have attended shift-1 and not shift-2, their raw marks in shift-2 will not be present. Similarly, the students (Stu1, Stu3, Stu5) who wrote the exam in shift-2, will have no marks in shift-1. These missing raw marks of each candidate in each shift are then calculated using a method called interpolation. Interpolation is a mathematical way of estimating missing raw marks of the students who are absent in one shift because they have already taken the test in the other shift. The Interpolated Marks (IMStu1 , IMStu2 , IMStu3 , IMStu4 , IMStu5 , IMStu6) of the students are now shown in the table below.

(Graphics by Abhishek Mitra)

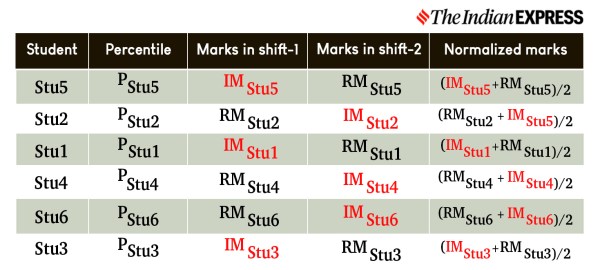
Using the above method, each percentile value of the candidates, sorted in descending order, will have marks for both shifts, raw marks where available and interpolated marks where not available because the student could not have written the test for a second time in the same subject. For each student, we then calculate the average of the actual raw marks in one shift and the raw marks obtained using interpolation in the other shift. This will give the normalised marks for the percentile of each candidate as shown below.

(Graphics by Abhishek Mitra)

This method has been shown to be accurate for estimating normalised marks of candidates when the tests are held in multiple sessions with varying difficulty levels in a given subject.

The scorecard of a candidate will have percentiles and normalised marks. Universities need to use the normalised marks given in the scorecard for preparing the rank list for admissions.

The above method is based on the work:

“Normalization of marks in multi-session examinations”, Abhay G. Bhatt et al, CURRENT SCIENCE, VOL. 118, NO. 1, 10 JANUARY 2020.